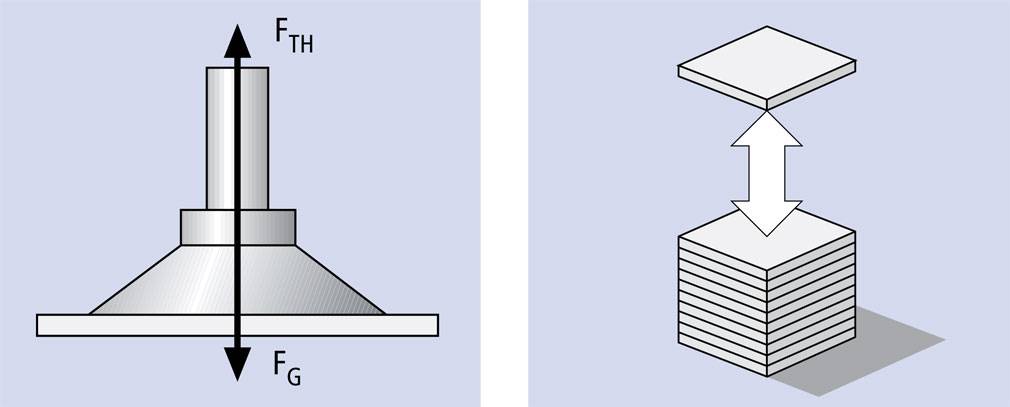
Theoretical Calculation of Negative Pressure
Formulation and Variables
The theoretical calculation of negative pressure for suction cups is governed by the formula:
[ P_{\text{max}} = \frac{10F}{S} ]
where:
- ( F ) represents the theoretical adsorption force, measured in Newtons (N).
- ( P_{\text{max}} ) denotes the maximum achievable negative pressure, expressed in kilopascals (kPa).
- ( S ) is the contact area between the suction cup and the object, quantified in square centimeters (cm²).
This formula provides a foundational understanding of how the theoretical maximum negative pressure is derived, which is essential for selecting appropriate vacuum pumps and ensuring effective object adsorption.
Limitations in Practical Applications
In practical applications, the theoretical calculations of negative pressure do not always translate directly into real-world performance. Several critical factors must be taken into account to ensure the effective operation of vacuum pumps, particularly in scenarios involving object adsorption.
Firstly, system sealing plays a pivotal role. Even minor leaks in the system can significantly reduce the actual suction force. This is because any breach in the seal allows air to seep back into the system, counteracting the negative pressure generated by the vacuum pump. Consequently, the effectiveness of the suction cups can be compromised, leading to potential failures in maintaining the adsorption of objects.
Secondly, surface adhesion is another crucial consideration. The ability of the suction cup to adhere to the object's surface is not solely dependent on the negative pressure but also on the surface characteristics. Smooth, non-porous surfaces generally provide better adhesion, while rough or porous surfaces can reduce the contact area, thereby diminishing the suction force. This variability in surface adhesion necessitates a more nuanced approach to vacuum pump selection.
Lastly, safety margins are essential to account for uncertainties and variations in real-world conditions. The theoretical calculations often assume ideal conditions, which may not hold true in practical applications. Therefore, incorporating safety margins ensures that the vacuum pump can handle unexpected fluctuations in pressure, flow rate, and surface conditions. This precautionary measure is particularly important in critical applications where failure could lead to significant consequences.
In summary, while theoretical calculations provide a foundational understanding of negative pressure, practical applications require a comprehensive consideration of system sealing, surface adhesion, and safety margins to ensure reliable and effective suction force.
Practical Considerations in Vacuum Pump Selection
Importance of Flow Rate
The actual flow rate of the vacuum pump is a critical parameter that directly influences the efficiency and reliability of the object adsorption process. This metric becomes especially significant when addressing the issue of air leakage between the suction cup and the object surface. Air leakage can compromise the vacuum pressure, thereby reducing the effectiveness of the suction force and potentially leading to failure in maintaining the grip.
To better understand the impact of flow rate, it is essential to consider the following key points:
-
Air Leakage Management: High flow rates help in quickly compensating for any air ingress, maintaining the required vacuum level. This is particularly important in applications where the object surface is not perfectly smooth or when there are minor deformities that could lead to air infiltration.
-
Dynamic Performance: In dynamic environments where objects are being moved or rotated, a higher flow rate ensures that the vacuum pressure is consistently maintained. This dynamic stability is crucial for tasks that require precision handling, such as automated assembly lines or robotic arms.
-
System Efficiency: A vacuum pump with an optimal flow rate not only enhances the system's performance but also contributes to energy efficiency. By maintaining a stable vacuum level with minimal energy consumption, the overall operational costs can be significantly reduced.
In summary, the selection of a vacuum pump with the appropriate flow rate is not just about meeting theoretical standards but also about ensuring practical robustness and reliability in real-world applications. This consideration is vital for industries that rely on precise and consistent object handling, where even minor discrepancies in vacuum pressure can lead to significant operational challenges.
Safety and Error Margins
To ensure the vacuum pump meets the rigorous demands of its application, it is imperative to select models with generous actual flow rates and elevated negative pressures. This proactive approach accounts for potential deviations and fluctuations that may arise during operation.
| Consideration | Impact on Safety Margins |
|---|---|
| Flow Rate | Ensures adequate suction even with minor air leaks. |
| Negative Pressure | Provides a buffer against variations in surface adhesion and system sealing. |
By opting for pumps with enhanced capabilities, users can navigate uncertainties more effectively, thereby safeguarding the integrity and reliability of the vacuum system.
Related Products
- Oil Free Diaphragm Vacuum Pump for Laboratory and Industrial Use
- Circulating Water Vacuum Pump for Laboratory and Industrial Use
- Laboratory Vertical Water Circulating Vacuum Pump for Lab Use
- Laboratory Benchtop Water Circulating Vacuum Pump for Lab Use
- Laboratory Rotary Vane Vacuum Pump for Lab Use
