What is the chirality diameter of a carbon nanotube? How Chirality Determines CNT Properties

In short, there is no standard term called "chirality diameter." Instead, the diameter of a carbon nanotube (CNT) is a direct physical consequence of its chirality, which describes the specific angle and geometry of its atomic structure. Chirality is defined by a pair of integers, (n,m), that dictate precisely how a sheet of graphene is conceptually "rolled up" to form the tube.

The core concept is that a carbon nanotube's diameter is not an arbitrary value but is a discrete property mathematically locked to its atomic structure. Understanding the (n,m) chiral indices allows you to calculate its exact diameter, which in turn predicts its fundamental electronic and physical properties.

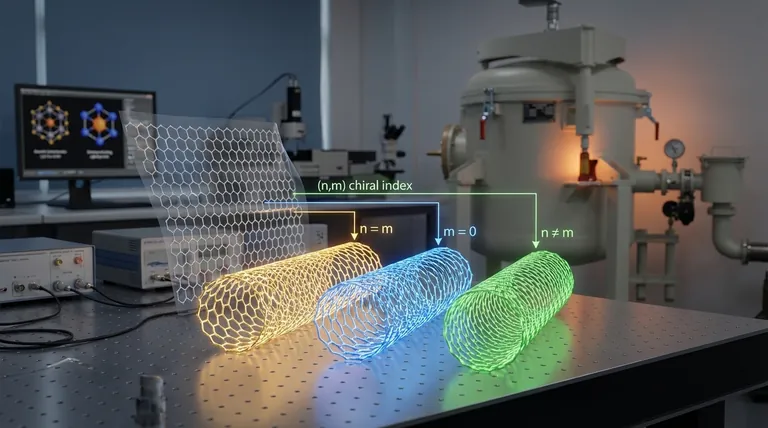
From Graphene Sheet to Nanotube

The Concept of Chirality

Imagine a flat sheet of graphene, a single layer of carbon atoms arranged in a honeycomb lattice. A carbon nanotube is formed by rolling this sheet into a seamless cylinder.

Chirality is the term used to describe the precise angle and direction in which you roll the sheet. This is not an arbitrary process; it is defined by a chiral vector, denoted as Ch.

The (n,m) Chiral Indices

The chiral vector is defined by two integers, (n,m), which represent the number of steps you take along the two primary directions in the graphene lattice to get from one point to an identical point after wrapping.

These indices uniquely define the nanotube's entire structure. Based on their values, CNTs are classified into three main types:

• Armchair: When n = m, e.g., (10,10).
• Zigzag: When m = 0, e.g., (17,0).
• Chiral: All other combinations where n ≠ m and m ≠ 0, e.g., (12,8).

Calculating the Diameter from Chirality

The Diameter Formula

Once you know the (n,m) indices of a nanotube, its diameter (d) can be calculated with a precise mathematical formula.

The formula is: d = (a / π) * √(n² + m² + nm)

This equation directly links the abstract (n,m) indices to a physical, measurable dimension.

Understanding the Variables

In the formula, 'a' is the graphene lattice constant. This value is derived from the fundamental carbon-carbon bond length (a_cc), which is approximately 0.142 nanometers (nm).

The lattice constant a is calculated as a = a_cc * √3, making it approximately 0.246 nm. The Greek letter π (pi) is the mathematical constant, approximately 3.14159.

Why Diameter Is a Critical Parameter

It Dictates Electronic Properties

The exact geometry determined by (n,m) and the resulting diameter has a profound effect on how electrons can travel through the nanotube. This directly determines if the CNT behaves like a metal or a semiconductor.

A simple rule of thumb is:

• Armchair (n,n) nanotubes are always metallic.
• For all other types, the nanotube is metallic if (n-m) is a multiple of 3.
• If (n-m) is not a multiple of 3, the nanotube is semiconducting.

This property is why CNTs are so promising for next-generation electronics; you can have a metallic wire or a semiconductor transistor component from the exact same element, just by changing its geometry.

It Influences Physical and Optical Properties

The diameter also affects the mechanical strength, stiffness, and the specific wavelengths of light that a nanotube will absorb or emit.

Smaller diameter tubes are generally stiffer, while the electronic band gap of semiconducting CNTs is inversely proportional to their diameter.

The Practical Challenge: Synthesis Control

The Problem of Mixed Chirality

The primary challenge in harnessing the power of CNTs is controlling their synthesis. Most production methods, like chemical vapor deposition (CVD), produce a mixture of nanotubes with many different (n,m) values.

This results in a sample containing a blend of different diameters, including both metallic and semiconducting tubes.

The Hurdle for Applications

This lack of uniformity is a major roadblock. For a computer chip, you need purely semiconducting nanotubes. For a transparent conductive film, you might want purely metallic ones.

Separating this mixture—a process called "sorting"—is a complex and expensive area of ongoing research. The inability to cheaply produce single-chirality CNTs at scale is what currently limits their widespread commercial application in electronics.

Making the Right Choice for Your Goal

• If your primary focus is creating a nanoscale electronic wire: You need a metallic CNT. The most reliable choice is an armchair (n,n) tube, as its metallic nature is guaranteed.
• If your primary focus is building a field-effect transistor (FET): You require a semiconducting CNT. You must select a (n,m) combination where (n-m) is not a multiple of 3.
• If your primary focus is on mechanical reinforcement in a composite material: A mixture of chiralities may be acceptable, but controlling the distribution of diameters can help optimize strength and load transfer.
• If your primary focus is on optical applications like sensors: You need a specific semiconducting CNT whose diameter provides the exact band gap required to interact with a target wavelength of light.

Ultimately, the power of the (n,m) indices is that they provide a direct blueprint from atomic structure to functional properties.

Summary Table:

CNT Type	Chirality (n,m)	Key Property
Armchair	n = m (e.g., 10,10)	Always metallic
Zigzag	m = 0 (e.g., 17,0)	Metallic if (n-m) is multiple of 3
Chiral	n ≠ m, m ≠ 0 (e.g., 12,8)	Semiconducting if (n-m) not multiple of 3

Ready to advance your carbon nanotube research? KINTEK provides precision lab equipment and consumables tailored for nanotechnology development. Whether you're synthesizing, characterizing, or applying CNTs, our solutions help you achieve the chirality control and material performance you need. Contact our experts today to discuss how we can support your laboratory's specific challenges in nanomaterials and beyond.