How do you calculate ball mill load? Optimize Grinding Efficiency and Reduce Costs

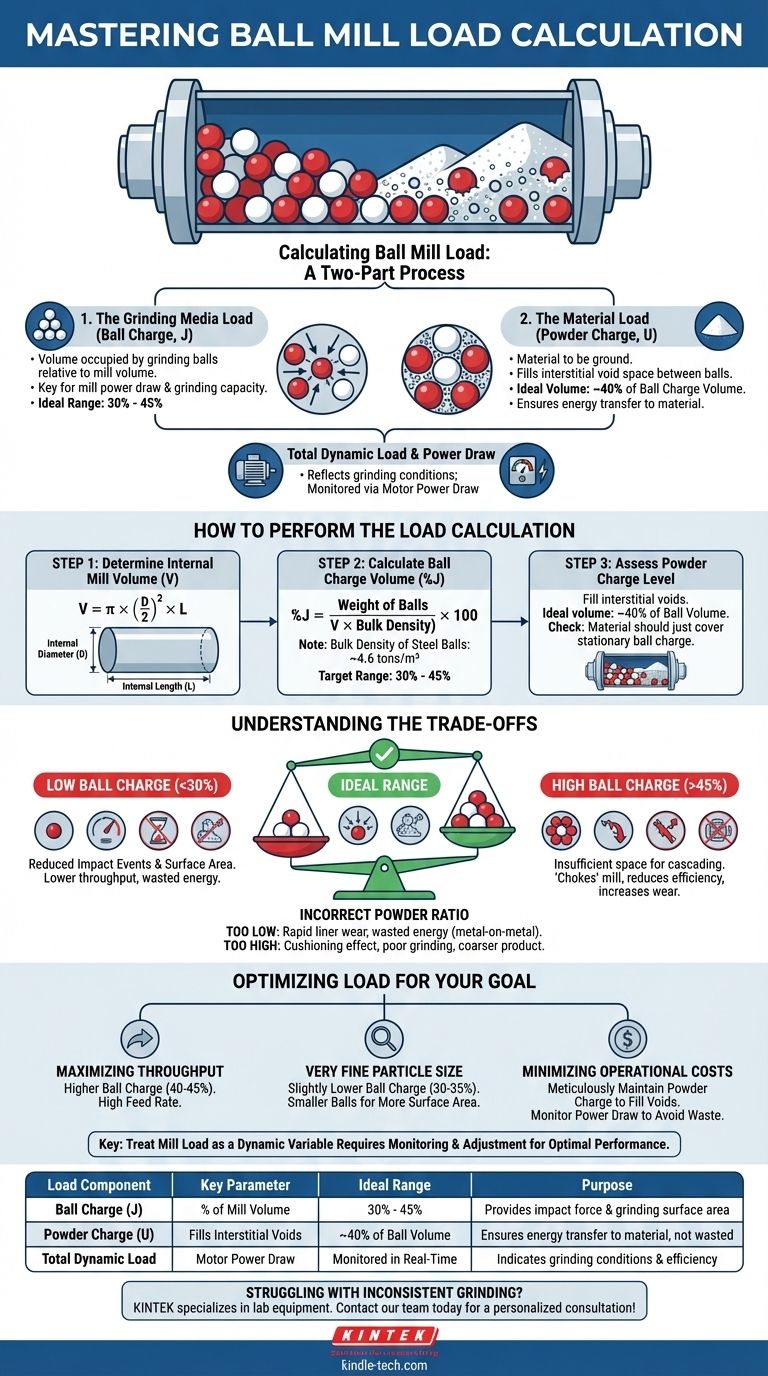
Calculating your ball mill load is a two-part process that involves determining the volume occupied by both the grinding media (the balls) and the material being processed (the powder). The most common and critical calculation is for the ball charge, which is expressed as a percentage of the total internal mill volume and is typically maintained between 30% and 45%.

Accurately calculating and managing your ball mill load is not just about filling the machine; it is the primary lever you have to control grinding efficiency, energy consumption, and the final particle size of your product. The key is to understand the distinct roles and ideal ratios of the ball charge and the powder charge.

Deconstructing Ball Mill Load: Balls vs. Powder

To control your process, you must first understand that "load" refers to two distinct but related components inside the mill.

The Grinding Media Load (Ball Charge, J)

The ball charge (J) is the total volume of the grinding balls relative to the internal volume of themill. This is the single most important parameter for determining mill power draw and grinding capacity.

A proper ball charge ensures there is sufficient surface area and weight for impact and attrition, the primary mechanisms of grinding.

The Material Load (Powder Charge, U)

The powder charge (U) is the material you are grinding. Its primary role is to fill the interstitial void space between the grinding balls.

The volume of this void space is approximately 40% of the volume occupied by the ball charge. Proper powder loading ensures energy is transferred from the balls to the material, rather than being wasted on metal-on-metal contact.

Total Dynamic Load and Power Draw

The combined weight of the balls and powder, along with the mill speed, determines the total dynamic load.

This load is directly reflected in the power consumed by the mill's motor. As a result, motor power draw is an excellent real-time indicator of the grinding conditions inside the mill.

How to Perform the Load Calculation

Follow these steps to determine the correct load for your ball mill.

Step 1: Determine Internal Mill Volume (V)

First, you need the precise internal volume of your mill, excluding the liners. The formula for a cylinder is:

V = π × (D/2)² × L

Here, D is the internal diameter of the mill, and L is the internal length.

Step 2: Calculate the Ball Charge Volume (%J)

The ball charge is calculated by weight and then converted to a volume percentage. The target is typically between 30% and 45%.

To calculate your current charge percentage, use this formula:

%J = (Weight of Balls / (Mill Volume × Bulk Density of Balls)) × 100

The bulk density of steel balls is approximately 4.6 tons per cubic meter (t/m³).

Step 3: Assess the Powder Charge Level

The powder charge should be sufficient to fill the void space between the balls. An insufficient charge leads to liner damage and energy waste, while an excessive charge cushions the balls and hinders grinding.

The ideal powder volume is roughly 40% of the ball charge volume. A quick way to check is by stopping the mill and observing the material level; it should be just covering the stationary ball charge.

Understanding the Trade-offs

Optimizing load is a balancing act. Deviating from the ideal range has direct consequences on performance and operational cost.

The Impact of a Low Ball Charge (<30%)

A low ball charge drastically reduces the number of impact events and the total grinding surface area.

This results in lower throughput, inefficient grinding, and wasted energy, as the mill lifts less weight than it was designed for.

The Impact of a High Ball Charge (>45%)

Overfilling the mill with balls leaves insufficient space for the charge to lift and cascade, which is essential for impact grinding.

This "chokes" the mill, reducing grinding efficiency and significantly increasing wear on the mill liners and the balls themselves due to increased abrasion.

The Problem of an Incorrect Powder Ratio

If the powder level is too low, the balls will strike each other and the mill liners directly. This causes rapid, costly wear and wastes a tremendous amount of energy as noise and heat.

If the powder level is too high, it creates a cushioning effect that absorbs the impact energy of the balls, leading to poor grinding and a much coarser final product.

Optimizing Load for Your Grinding Goal

There is no single perfect load; the ideal setup depends entirely on your operational objective. Use these guidelines to make a decision.

• If your primary focus is maximizing throughput: Operate with a ball charge in the higher end of the range (40-45%) and ensure your feed rate is high enough to maintain the correct powder-to-ball ratio.
• If your primary focus is achieving a very fine particle size (e.g., -200 mesh): Consider a slightly lower ball charge (30-35%) with smaller grinding balls to increase the total surface area for attrition grinding.
• If your primary focus is minimizing operational costs: Meticulously maintain the powder charge to just fill the interstitial voids. Monitor power draw to ensure you are not wasting energy on inefficient metal-on-metal contact.

Ultimately, treating mill load as a dynamic variable that requires monitoring and adjustment—not a fixed number—is the key to unlocking optimal performance.

Summary Table:

Load Component	Key Parameter	Ideal Range	Purpose
Ball Charge (J)	% of Mill Volume	30% - 45%	Provides impact force and grinding surface area
Powder Charge (U)	Fills Interstitial Voids	~40% of Ball Volume	Ensures energy is transferred to material, not wasted
Total Dynamic Load	Motor Power Draw	Monitored in Real-Time	Indicates grinding conditions and efficiency

Struggling with inconsistent grinding results or high energy costs? KINTEK specializes in lab equipment and consumables, serving laboratory needs. Our experts can help you select the ideal ball mill and grinding media to achieve precise particle size control and maximize your operational efficiency. Contact our team today for a personalized consultation!