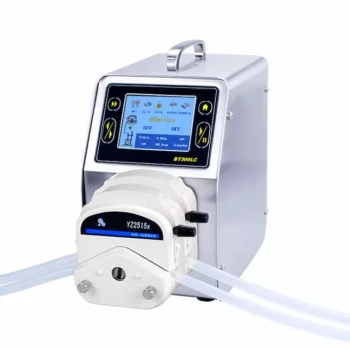
The definitive answer is false. Liquid pressure at a specific depth does not depend on the size or shape of its container. This is a fundamental principle of fluid statics. The pressure exerted by a fluid at rest is determined exclusively by its depth, its density, and the acceleration due to gravity, not the container's width, volume, or complex geometry.
The core principle to grasp is that liquid pressure is a function of the vertical height of the fluid column directly above the point of measurement. This concept, often called the hydrostatic paradox, means a thin, tall tube of water can exert the same pressure at its base as a wide lake of the same depth.
The Core Principles of Hydrostatic Pressure
To understand why the container's shape is irrelevant, we must first establish what does determine the pressure within a static (non-moving) fluid.
The Decisive Role of Depth (h)
Pressure originates from the weight of the fluid. At any given point, the pressure is caused by the weight of the column of fluid directly above it pushing down.
The deeper you go, the taller this column of fluid is, meaning more weight is pressing down from above. This is why pressure increases linearly with depth.
The Influence of Fluid Density (ρ)
Density is the measure of mass per unit of volume. A denser fluid, like mercury, has more mass packed into the same space than a less dense fluid like water.
Therefore, a column of a denser fluid will be heavier and exert more pressure than a column of the same height of a less dense fluid.
The Constant of Gravity (g)
Gravity is the force that pulls the fluid's mass downward, creating the weight that results in pressure. While it varies slightly across the Earth, for most practical purposes, it is considered a constant.
These three factors—depth (h), density (ρ), and gravity (g)—are combined in the foundational formula for hydrostatic pressure: P = ρgh. Notice that no variable in this equation accounts for the container's volume or shape.
Why Container Shape and Size Are Irrelevant
The idea that the shape of a container doesn't affect pressure at its base can seem counter-intuitive. A huge tank of water clearly contains more total weight than a narrow pipe. The key is to distinguish between pressure and total force.
The Hydrostatic Paradox
This principle states that the pressure at the bottom of a set of interconnected containers of different shapes will be the same, as long as the fluid height is the same in all of them.
The total weight of the fluid in a wide tank is much greater, but that weight is distributed over a much larger area. The weight in the narrow pipe is small, but it is concentrated on a very small area. The ratio of force to area (pressure) remains the same.
Force vs. Pressure
Pressure is defined as force per unit area (P = F/A).
In a wide container, the container's bottom supports the weight of the water directly above it. The slanted walls or the floor of the container support the rest of the water's weight. The pressure at any single point on the bottom is only affected by the fluid column directly over that point.
A Practical Analogy
Imagine three single stacks of books on a table. One stack has 10 books. The next has 10 identical books. The third also has 10 identical books.
The pressure on the book at the bottom of each stack is identical. It doesn't matter if the stacks are placed far apart or close together on the table. The pressure on the bottom book only depends on the weight of the books in its own stack, not the total number of books on the table.
Common Pitfalls and Misconceptions
Understanding this principle requires avoiding a few common points of confusion.
Confusing Pressure with Total Force
While pressure at the bottom of a dam depends only on the water's depth, the total force the dam must withstand absolutely depends on its size (surface area).
Engineers calculate the pressure at various depths and then integrate that pressure over the dam's entire surface area to find the total force it must resist. The force is greater on a wider dam, but the pressure at a 20-meter depth remains the same regardless.
Dynamic vs. Static Fluids
This entire discussion applies to hydrostatics—fluids at rest. If a fluid is in motion (hydrodynamics), other factors like velocity come into play, and the pressure relationship becomes more complex, as described by principles like Bernoulli's equation.
The Small-Scale Exception: Surface Tension
In extremely narrow tubes (capillaries), surface tension can have a measurable effect on the fluid's behavior. However, for the vast majority of macroscopic applications, from a water glass to an oceanic trench, this effect is negligible.
Making the Right Choice for Your Goal
Applying this concept correctly depends on the problem you are trying to solve.
- If your primary focus is engineering a structure (like a tank or dam): Your material strength calculations must be based on the maximum fluid depth, as this determines the maximum pressure the structure will endure at its base.
- If your primary focus is academic understanding: Remember that pressure is force per unit area, and the supporting forces from the container walls are what makes the container's overall shape irrelevant to the pressure at a single point.
- If your primary focus is hydraulics (like in a car lift): This principle is the foundation of Pascal's Law, where pressure applied to an enclosed fluid is transmitted undiminished, allowing a small force on a small piston to generate a large force on a large piston.
Ultimately, internalizing that pressure is a function of depth, not volume, is the key to accurately predicting the behavior of fluids at rest.
Summary Table:
| Factor | Effect on Liquid Pressure |
|---|---|
| Depth (h) | Pressure increases linearly with depth. |
| Fluid Density (ρ) | Denser fluids exert greater pressure at the same depth. |
| Gravity (g) | The constant force that creates pressure from the fluid's weight. |
| Container Shape/Size | No effect on pressure at a specific depth. |
Need precise control over fluid pressure in your lab processes? Understanding hydrostatic principles is key to selecting the right equipment. KINTEK specializes in high-quality lab equipment and consumables that ensure accurate and reliable performance for all your fluid handling and analysis needs. Let our experts help you build a safer, more efficient laboratory. Contact us today to discuss your specific requirements!
Visual Guide
