How Does The Sample Size Affect The Needed Accuracy Of The Measurement? Optimize Your Data Quality

In short, a larger sample size does not change the inherent accuracy of your measurement instrument, but it dramatically increases the accuracy of the conclusions you can draw from your data. By collecting more samples, you reduce the "sampling error," which is the uncertainty that comes from observing a part of a group instead of the whole. This means your results are more likely to be a true representation of the entire population.

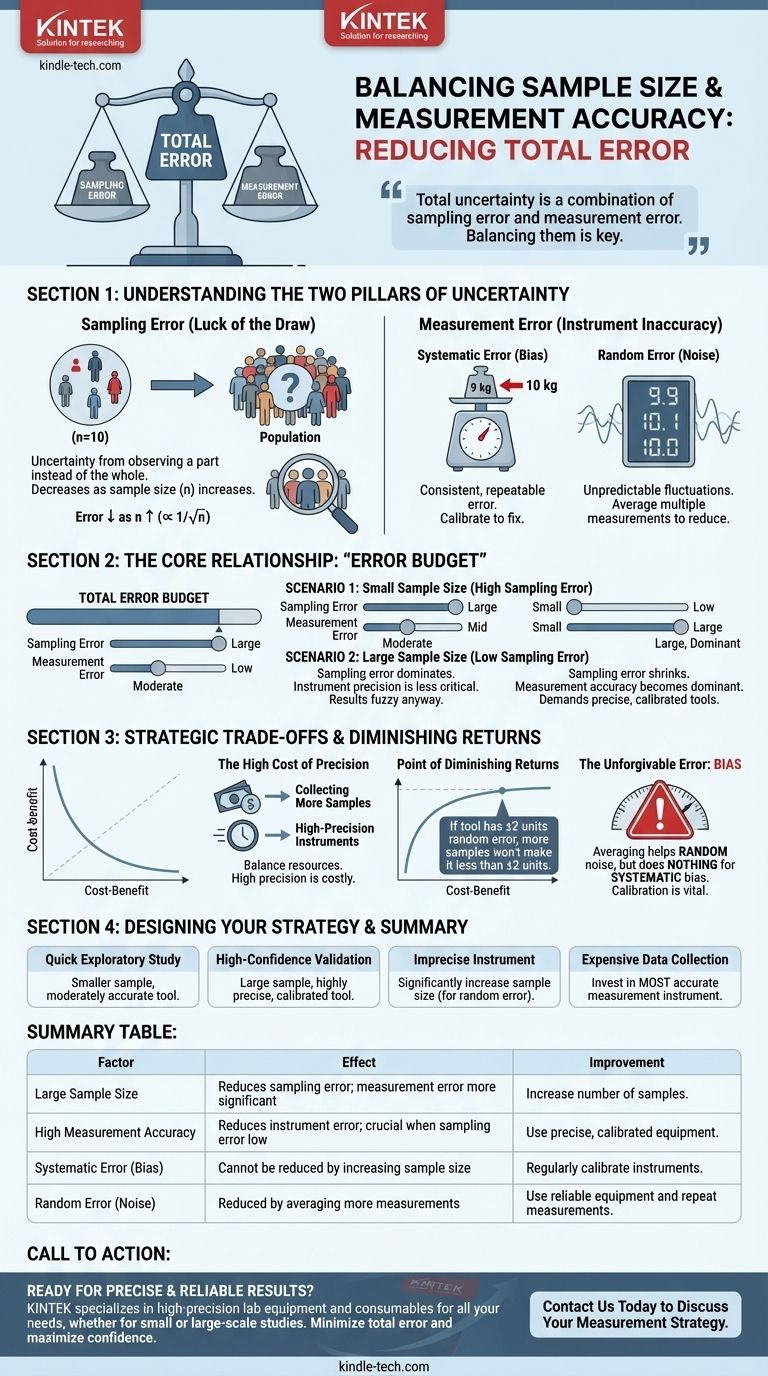
The core issue isn't just about sample size; it's about balancing two distinct sources of error. Your total uncertainty is a combination of sampling error (from the size of your sample) and measurement error (from the quality of your tool). Understanding how these two interact is the key to designing an effective study.

The Two Pillars of Uncertainty: Sampling vs. Measurement

To grasp the relationship fully, you must distinguish between the two fundamental types of error that can affect your results. They are not interchangeable.

Understanding Sampling Error

Sampling error is the "luck of the draw." It's the random difference between the characteristics of your sample and the characteristics of the entire population it's meant to represent.

Imagine trying to determine the average height of all people in a city by measuring only 10 individuals. You might accidentally pick an unusually tall or short group.

This error is not a mistake; it's a statistical reality. The good news is that it is predictable and can be controlled. As your sample size (n) increases, your sampling error decreases at a rate proportional to the square root of the sample size (1/√n). A larger sample is more likely to mirror the true population.

Understanding Measurement Error

Measurement error is the inaccuracy inherent in your measurement device or method. It has nothing to do with how many samples you take.

This error comes in two forms:

Systematic Error (Bias): A consistent, repeatable error. Think of a scale that always reads 1 kg too high. Taking more measurements won't fix this; you'll just get a very precise, but wrong, answer.
Random Error (Noise): Unpredictable fluctuations in measurement. Think of a digital scale whose last digit flickers slightly.

Averaging many measurements can help reduce the effect of random error, but it can never correct for systematic error. The accuracy of your tool creates a hard limit on the ultimate truthfulness of your data.

How Sample Size and Measurement Accuracy Interact

The crucial insight is that these two errors contribute to your total "error budget." Your goal is to minimize total error, and how you allocate resources to fight each type of error depends on your situation.

The Core Relationship: Your "Error Budget"

Think of your desired level of confidence as a budget for total error. You "spend" this budget on a combination of sampling error and measurement error.

If one source of error is very large, it will dominate your results, and reducing the other source may have little practical effect.

Scenario 1: Small Sample Size

When your sample size is small, sampling error is high. It is almost always the largest contributor to your total uncertainty.

In this situation, the precision of your measurement tool is less critical. Your result will be fuzzy anyway due to the "luck of the draw" in sampling, so a small amount of measurement error won't make the overall picture much worse.

Scenario 2: Large Sample Size

As you increase your sample size, the sampling error shrinks dramatically. Your sample average gets closer and closer to the true population average.

This is where the user's question becomes particularly insightful. A large sample size effectively increases the demand for accurate measurement. As sampling error disappears, any error from your instrument becomes the dominant source of uncertainty.

If your measurement tool has a systematic bias, a huge sample size will just give you a very precise estimate of the wrong value. It magnifies the importance of having a well-calibrated and accurate instrument.

Understanding the Trade-offs

Deciding on sample size and instrument quality is a strategic balancing act, often dictated by time and money.

The High Cost of Precision

Collecting more samples costs time and resources. Likewise, high-precision, perfectly calibrated instruments are expensive. You must decide where to invest.

Pouring money into a massive sample size is wasteful if your results are ultimately limited by a cheap, inaccurate measurement tool.

The Point of Diminishing Returns

There is a point where increasing sample size yields almost no benefit. If your measurement tool has an inherent random error of ±2 units, you can never achieve a final confidence interval smaller than that, no matter how many samples you take.

Similarly, buying a multi-million dollar instrument is pointless if you only plan to take three samples, as your massive sampling error will dwarf the instrument's incredible precision.

The Unforgivable Error: Bias

Remember that increasing sample size helps average out random noise but does absolutely nothing to fix systematic bias.

Calibrating your instruments to eliminate systematic error is often the single most important step you can take to ensure the integrity of your data, regardless of sample size.

Designing Your Measurement Strategy

There is no single "correct" sample size or accuracy level. The right choice depends entirely on your objective and constraints.

If your primary focus is a quick exploratory study: A smaller sample size combined with a moderately accurate instrument may be sufficient to identify major trends and guide future research.
If your primary focus is high-confidence validation (e.g., regulatory approval): You need both a large, carefully selected sample and a highly precise, calibrated instrument to minimize both sampling and measurement error to a verifiable degree.
If your measurement instrument is known to be imprecise: You can compensate by significantly increasing your sample size, but only if the error is random, not systematic. This will reduce your overall uncertainty, but only up to the limit set by the instrument's flaws.
If collecting samples is extremely expensive or difficult (e.g., space exploration): You must invest in the most accurate measurement instrument possible to extract the maximum value from every precious data point.

Ultimately, balancing sample size and measurement accuracy is about strategically allocating your resources to combat the most significant sources of uncertainty in your specific context.

Summary Table:

Factor	Effect on Results	How to Improve
Large Sample Size	Reduces sampling error; makes measurement error more significant.	Increase the number of samples measured.
High Measurement Accuracy	Reduces instrument error; crucial when sampling error is low.	Use precise, well-calibrated equipment.
Systematic Error (Bias)	Cannot be reduced by increasing sample size.	Regularly calibrate instruments.
Random Error (Noise)	Can be reduced by averaging more measurements.	Use reliable equipment and repeat measurements.

Ready to achieve precise and reliable results in your lab?

The right balance of sample size and measurement accuracy is critical for the integrity of your data. KINTEK specializes in high-precision lab equipment and consumables, serving all your laboratory needs. Whether you require instruments with superior accuracy for small sample sets or robust equipment for large-scale studies, we have the solution to minimize your total error and maximize confidence in your findings.

Contact us today to discuss how our products can enhance your measurement strategy. Let our experts help you select the perfect tools for your specific application.

#ContactForm