Does increasing the insulation thickness increase the rate of heat transfer? The Critical Radius Explained

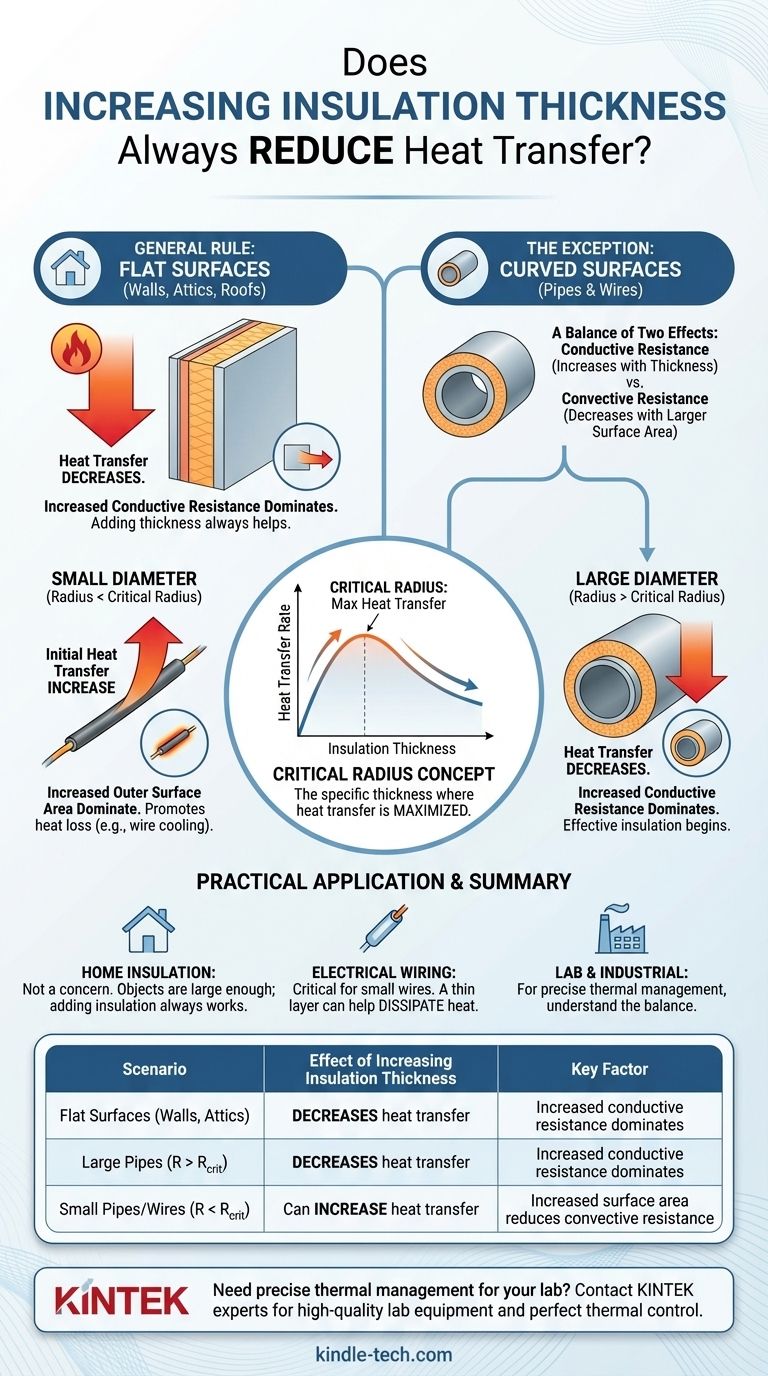
In almost all common applications, increasing the thickness of your insulation will decrease the rate of heat transfer. This is the fundamental purpose of insulation. However, for curved surfaces with a very small diameter, such as electrical wires or small pipes, there is a counterintuitive scenario where adding a thin layer of insulation can actually increase the rate of heat transfer due to a principle known as the critical radius of insulation.

The effectiveness of insulation depends on the balance between two competing effects: the resistance of heat flowing through the material (conduction) and the ease of heat escaping from its outer surface (convection). For most practical purposes like insulating a home, adding thickness always helps.

The Fundamental Goal of Insulation: Adding Resistance

To understand how insulation works, it's helpful to think of heat flow like electricity. Heat, like current, will always follow the path of least resistance. The job of insulation is to add thermal resistance to that path.

Understanding Thermal Resistance

Heat transfer is slowed by thermal resistance. The higher the total resistance, the lower the rate of heat transfer. Insulation effectiveness is measured by its R-value, which is a direct measure of its thermal resistance.

The Two Types of Resistance at Play

When you insulate an object, you are manipulating two key forms of resistance:

1. Conductive Resistance: This is the resistance to heat flowing through the solid insulation material. It increases directly with thickness. More material means more path for the heat to travel, which means higher resistance.
2. Convective Resistance: This is the resistance to heat moving from the insulation's outer surface to the surrounding air. This resistance decreases as the surface area gets larger, because a bigger surface gives the heat more area from which to escape.

Why Thickness Matters Differently for Walls vs. Pipes

The geometry of the surface you are insulating determines how these two resistances interact. This is the key to understanding why the answer to the question can be complex.

For Flat Surfaces (Walls, Attics, Roofs)

When you add insulation to a flat surface like a wall, you significantly increase the conductive resistance.

However, the outer surface area remains virtually unchanged. Therefore, the convective resistance is not affected. The net result is simple: total resistance goes up, and heat transfer goes down.

For Curved Surfaces (Pipes and Wires)

When you add insulation around a pipe or wire, you are doing two things at once:

1. You increase the conductive resistance by adding material thickness (which reduces heat transfer).
2. You increase the outer surface area, which decreases the convective resistance (which promotes heat transfer).

These two effects work against each other. The winner of this "tug-of-war" determines whether the net heat transfer rate goes up or down.

The Concept of the Critical Radius

The critical radius of insulation is the specific outer radius at which the heat transfer rate is at its absolute maximum.

• If the pipe's original radius is smaller than the critical radius: Adding insulation will initially increase heat loss. The negative effect of the growing surface area (less convective resistance) outweighs the positive effect of the added thickness (more conductive resistance).
• If the pipe's original radius is larger than the critical radius: Adding insulation will immediately begin to decrease heat loss, as it should. The benefit of increased conductive resistance is dominant from the start.

Understanding the Trade-offs: Critical Radius in Practice

While this phenomenon is an important concept in heat transfer physics, its practical application is limited to specific scenarios.

When is Critical Radius a Real Concern?

The critical radius effect is primarily relevant for objects with a very small diameter. For typical insulation materials, the critical radius is often only a few millimeters.

This makes it a factor in the design of electrical wiring, where the goal is often to dissipate heat to prevent overheating. A thin coating of insulation can actually help cool the wire more effectively than if it were bare. It is also a consideration for very small-bore process pipes, like steam tracer lines.

Why It's Rarely an Issue for Home Insulation

For nearly all household and commercial applications, the objects being insulated are already much larger than the critical radius.

A standard plumbing pipe, an HVAC duct, or a water heater is far too large for this effect to be a concern. For these items, you are already "over the hump," and adding any amount of insulation will reliably decrease heat transfer and save energy.

Making the Right Choice for Your Goal

Your approach to insulation should be guided by your specific application and desired outcome.

• If your primary focus is insulating your home (walls, attic, large pipes): Adding more insulation will reliably decrease heat transfer and lower energy bills. The critical radius is not a practical concern.
• If your primary focus is designing for small-diameter pipes or electrical wires: You must calculate the critical radius to ensure your insulation is achieving the desired effect, whether that is retaining or dissipating heat.
• If your primary focus is simply understanding the physics: Remember that the total heat transfer is determined by the balance between conduction (resisted by thickness) and convection (aided by surface area).

Understanding this balance between material resistance and surface area empowers you to use insulation effectively in any scenario.

Summary Table:

Scenario	Effect of Increasing Insulation Thickness	Key Factor
Flat Surfaces (Walls, Attics)	Decreases heat transfer	Increased conductive resistance dominates
Large Pipes (Radius > Critical Radius)	Decreases heat transfer	Increased conductive resistance dominates
Small Pipes/Wires (Radius < Critical Radius)	Can increase heat transfer	Increased surface area reduces convective resistance

Need precise thermal management for your lab equipment? Understanding heat transfer principles is crucial for maintaining optimal conditions for sensitive instruments and experiments. KINTEK specializes in providing high-quality lab equipment and consumables designed for efficiency and reliability. Whether you're insulating a reactor or selecting the right furnace, our expertise can help you achieve perfect thermal control. Contact our experts today to discuss your specific laboratory needs and enhance your lab's performance.