How much force can a hydraulic cylinder produce? Unlock the Power of Hydraulic Force Calculations

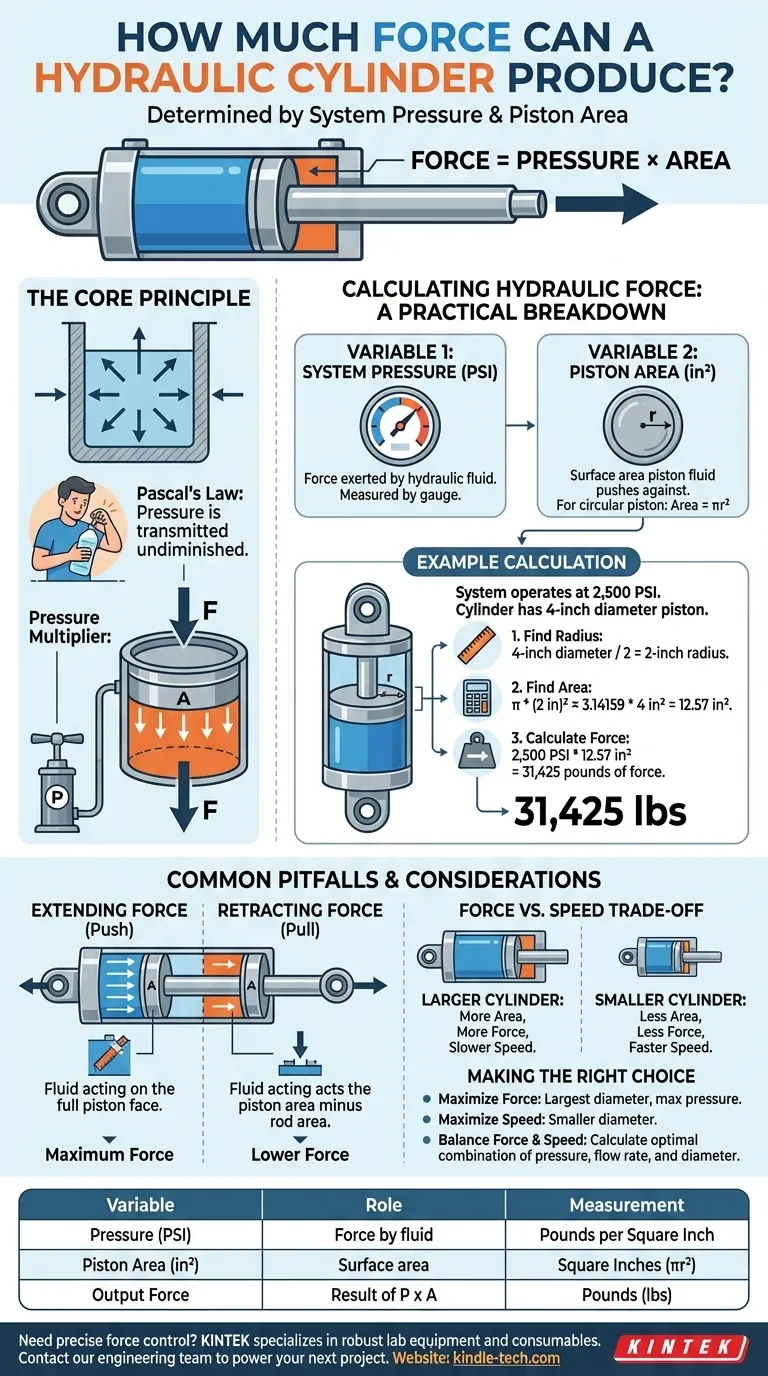
The force a hydraulic cylinder can produce is determined by a simple formula: it is the system's fluid pressure multiplied by the effective surface area of the piston. Therefore, the output force can be increased by either raising the system's pressure or by using a cylinder with a larger piston diameter.

The core principle is that hydraulic systems are force multipliers. They convert fluid pressure acting over a large area (the piston) into a powerful linear force, with the exact output being a direct and predictable result of pressure and piston size.

The Core Principle: How Hydraulics Multiply Force

Understanding Pascal's Law

The foundation of all hydraulics is Pascal's Law, which states that pressure applied to a confined fluid is transmitted undiminished to every portion of the fluid and the walls of the containing vessel.

Imagine squeezing a sealed plastic bottle full of water. The pressure you apply with your hand is felt equally on every single interior surface of that bottle.

A hydraulic cylinder works the same way. The hydraulic pump generates pressure (e.g., 2,000 pounds per square inch), and that pressure pushes equally on all internal surfaces, including the face of the piston.

From Pressure to Usable Force

The magic happens when this uniform pressure acts upon the large surface area of the piston. A small amount of pressure, spread over a wide area, consolidates into a large, usable output force.

This is why even a small hydraulic pump can generate enough pressure to lift incredibly heavy loads like a car or an excavator bucket.

Calculating Hydraulic Force: A Practical Breakdown

The Two Critical Variables

To calculate the output force, you only need to know two things: the system's pressure and the piston's area.

The formula is: Force = Pressure x Area

Variable 1: System Pressure

Pressure, measured in Pounds per Square Inch (PSI), is the force exerted by the hydraulic fluid. This is generated by the system's pump. For calculations, you will use the pressure reading from the system's gauge.

Variable 2: Piston Area

Area, measured in square inches (in²), is the surface area of the piston face that the fluid pushes against.

Because pistons are circular, you calculate this using the formula for the area of a circle: Area = πr², where 'r' is the radius of the piston (half its diameter). A larger cylinder diameter results in a larger piston area.

Putting It Together: An Example

Let's say your system operates at 2,500 PSI and you have a cylinder with a 4-inch diameter piston.

1. First, find the radius: 4-inch diameter / 2 = 2-inch radius.
2. Next, calculate the area: π * (2 in)² ≈ 3.14159 * 4 in² = 12.57 in².
3. Finally, calculate the force: 2,500 PSI * 12.57 in² = 31,425 pounds of force.

Common Pitfalls and Considerations

Extending vs. Retracting Force

A cylinder does not produce the same amount of force in both directions.

• Extending Force (Push): When the cylinder pushes, the fluid acts on the full face of the piston. This is where the calculation above applies, and it represents the cylinder's maximum theoretical force.
• Retracting Force (Pull): When the cylinder pulls, the piston rod is in the way. The fluid can only act on the surface area of the piston minus the area of the rod. This results in a lower output force during retraction.

The Force vs. Speed Trade-off

For a given pump flow rate, force and speed have an inverse relationship.

A larger cylinder (more area) will produce more force but will move slower because it requires more fluid to fill the same stroke length. A smaller cylinder will be faster but produce less force.

Making the Right Choice for Your Goal

• If your primary focus is maximizing force: Select the cylinder with the largest piston diameter that fits your design and operate your system at its maximum safe pressure rating.
• If your primary focus is speed: A smaller diameter cylinder will move faster for a given fluid flow rate, though it will produce less force.
• If you must balance force and speed: You will need to carefully calculate the optimal combination of system pressure, pump flow rate, and cylinder diameter to meet the specific demands of your application.

Understanding these core principles allows you to precisely control and predict the powerful forces at your command.

Summary Table:

Variable	Role in Force Calculation	Measurement
Pressure (PSI)	Force exerted by the hydraulic fluid	Pounds per Square Inch
Piston Area (in²)	Surface area the fluid pushes against	Square Inches (πr²)
Output Force	Result of Pressure x Area	Pounds (lbs)

Example Calculation (2,500 PSI, 4" Piston)

Step	Calculation	Result
1. Find Radius	4" diameter / 2	2 inches
2. Find Area	π * (2 in)²	12.57 in²
3. Calculate Force	2,500 PSI * 12.57 in²	31,425 lbs

Need precise force control for your lab or industrial application? The principles of hydraulic force are fundamental to many powerful systems. At KINTEK, we specialize in providing robust lab equipment and consumables that rely on precise mechanical principles. Whether you're designing a new system or optimizing an existing one, our expertise can help you achieve reliable and accurate results.

Contact our engineering team today to discuss how KINTEK's solutions can power your next project.

Visual Guide