How do you convert hydraulic pressure to force? Master the Core Formula for Maximum Power

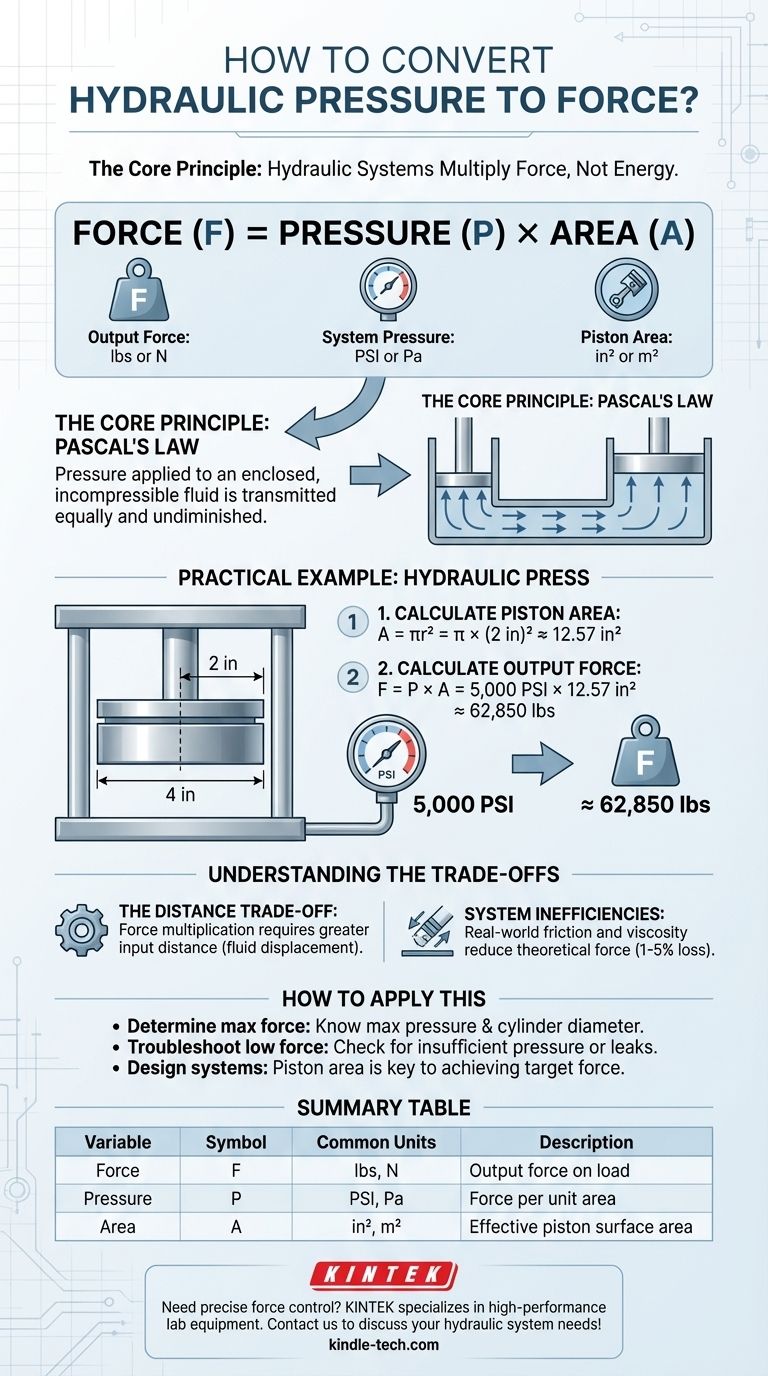
The direct formula for converting hydraulic pressure into force is Force = Pressure × Area. To find the total force a hydraulic system can exert, you multiply the system's pressure (often measured in Pounds per Square Inch or PSI) by the effective surface area of the component being acted upon, such as a piston. This simple relationship is the foundation of all hydraulic power.

The core principle to understand is that hydraulic systems do not create energy; they multiply force. By applying a given pressure across a large surface area (like a large piston), you can convert a manageable pressure into an immense output force.

The Core Principle: Pascal's Law

The formula for converting pressure to force is a direct application of a fundamental concept in fluid mechanics known as Pascal's Law.

What is Pascal's Law?

Pascal's Law states that pressure applied to an enclosed, incompressible fluid is transmitted equally and undiminished to every part of the fluid and the walls of its container.

In a hydraulic system, the oil is the enclosed fluid. When you pump the handle on a hydraulic press, you are pressurizing that oil. That pressure is then exerted equally on all internal surfaces, including the large piston that does the work.

Defining the Variables

To use the formula correctly, you must be precise about the units.

• Force (F): This is the output you are calculating, often expressed in pounds (lbs) or Newtons (N). It represents the total load the system can apply to a workpiece.
• Pressure (P): This is the force per unit of area within the system. It is almost always measured in Pounds per Square Inch (PSI) or Pascals (Pa). This is the value you would read on the system's pressure gauge.
• Area (A): This is the surface area of the component the pressure is acting upon, typically the face of the main piston. It must be measured in square inches (in²) or square meters (m²) to align with your pressure unit.

A Practical Example: The Hydraulic Press

Let's apply this formula to a common piece of equipment, like the hydraulic press mentioned in the reference materials.

Step 1: Calculate the Piston Area

Most hydraulic cylinders use a circular piston. The formula for the area of a circle is A = πr², where 'r' is the radius of the piston.

Imagine your press has a large piston with a diameter of 4 inches. Its radius is half of that, which is 2 inches.

The area would be: A = π × (2 in)² ≈ 12.57 in²

Step 2: Calculate the Output Force

Now, assume you pump the system until the pressure gauge reads 5,000 PSI.

Using the core formula, Force = Pressure × Area:

Force = 5,000 lbs/in² × 12.57 in² ≈ 62,850 lbs

By applying 5,000 PSI of pressure to a 4-inch diameter piston, the press can exert nearly 63,000 pounds of force.

Understanding the Trade-offs

This force multiplication seems almost magical, but it comes at a cost that is dictated by the laws of physics.

The Trade-off is Distance

You do not get more work out of the system than you put in. The trade-off for multiplying force is the distance the fluid must travel.

To move the large 12.57 in² piston by just one inch, you must displace 12.57 cubic inches of hydraulic fluid. If the input piston you are pumping has an area of only 0.5 in², you would need to push it a distance of over 25 inches to achieve that single inch of movement on the output side.

System Inefficiencies Matter

The formula F = P × A calculates the theoretical maximum force. In any real-world system, you will achieve slightly less.

Factors like friction from the piston seals rubbing against the cylinder wall and the internal viscosity of the hydraulic fluid will consume some of the energy. These losses are typically small (1-5%) in a well-maintained system but are important to acknowledge.

How to Apply This to Your Project

Understanding this principle allows you to make informed decisions when using or evaluating hydraulic equipment.

• If your primary focus is determining the maximum force of your equipment: You must know two numbers: the maximum rated system pressure (in PSI) and the diameter of the main cylinder to calculate its area.
• If your primary focus is troubleshooting a low-force issue: The problem is almost certainly either insufficient pressure (from a failing pump or an incorrectly set relief valve) or a loss of pressure due to internal leaks.
• If your primary focus is designing or selecting a hydraulic system: The piston area is your most powerful design choice for achieving a target force from a standard operating pressure.

This fundamental equation is the key to safely harnessing and controlling the immense power of hydraulic systems.

Summary Table:

Variable	Symbol	Common Units	Description
Force	F	Pounds (lbs), Newtons (N)	The total output force exerted on the load.
Pressure	P	PSI, Pascals (Pa)	The force per unit area within the hydraulic fluid.
Area	A	in², m²	The effective surface area of the piston the pressure acts upon.

Need precise force control for your lab or production line? The principles of hydraulic force are critical for operating equipment safely and efficiently. At KINTEK, we specialize in high-performance lab equipment, including hydraulic presses and consumables designed for reliability and accurate force output. Let our experts help you select the right equipment for your specific application. Contact KINTALK today to discuss your hydraulic system needs!

Visual Guide