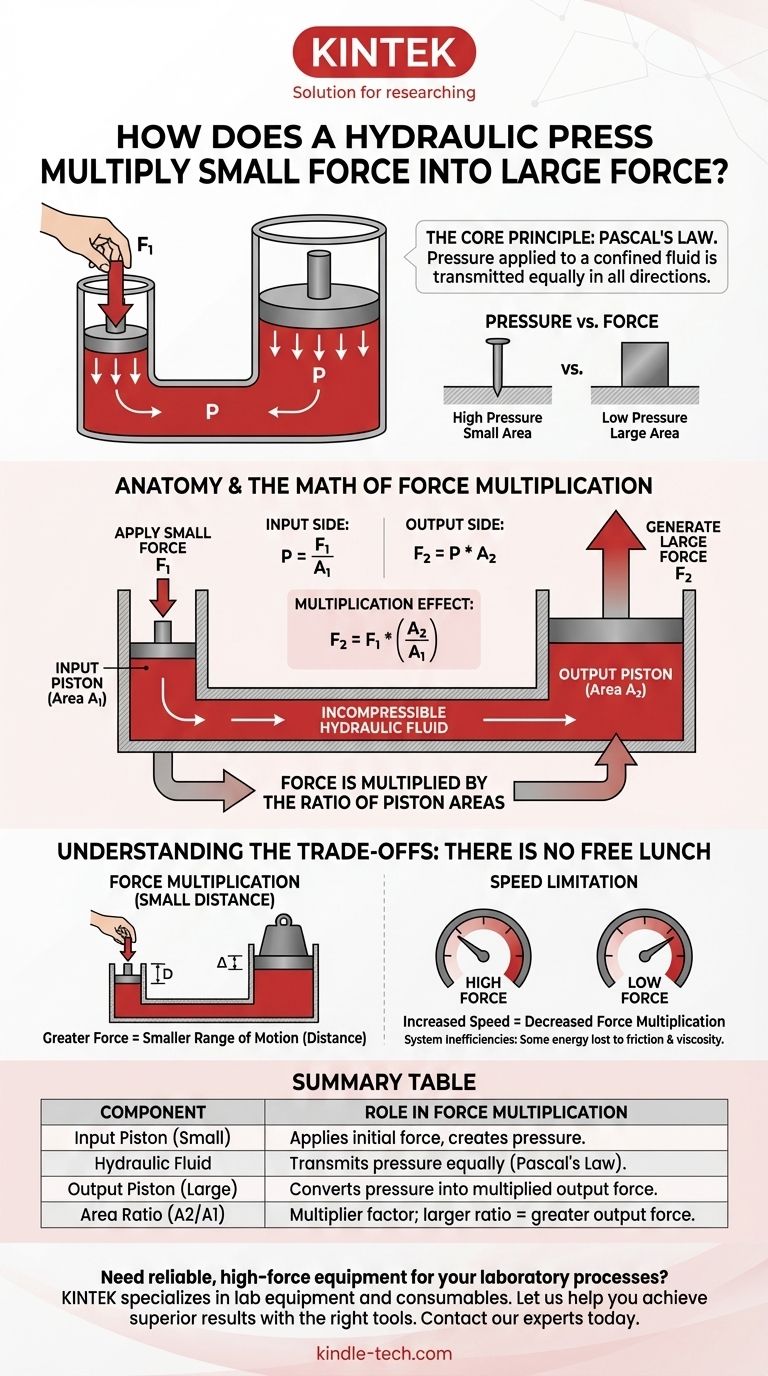
At its core, a hydraulic press multiplies force by using a confined, incompressible fluid to transfer pressure from a small area to a large area. When you apply a small force to a small piston, you create pressure in the fluid. According to Pascal's Principle, this pressure is distributed equally throughout the fluid, and when it acts on a second, much larger piston, it generates a proportionally larger output force.
The secret to hydraulic force multiplication is not the creation of new energy, but the strategic trade-off between force and distance. A constant pressure is simply applied over a larger surface area to produce a greater force, at the cost of a smaller range of motion.
The Core Principle: Understanding Pascal's Law
The entire function of a hydraulic press is built upon a fundamental law of fluid mechanics discovered by Blaise Pascal in the 17th century.
What is Pressure?
First, it's critical to distinguish between force and pressure. Force is a push or a pull on an object. Pressure is defined as force distributed over a specific unit of area (Pressure = Force / Area).
A 100-pound weight resting on a sharp nail point creates immense pressure, while the same weight spread across a large wooden board creates very little pressure.
How Pascal's Law Works
Pascal's Law states that a pressure change at any point in a confined, incompressible fluid is transmitted equally and undiminished to every portion of the fluid.
Think of a sealed water balloon. If you squeeze one end, the entire balloon becomes firm, not just the part you are squeezing. The pressure you apply is transmitted everywhere inside. This is the principle that hydraulic systems exploit.
Anatomy of a Hydraulic Press
A simple hydraulic press has three key components that work together to apply this principle.
The Input Piston (Small Piston)
This is where a small, initial force is applied. Because this piston has a small surface area, even a modest force can generate significant pressure in the hydraulic fluid.
The Output Piston (Large Piston)
This piston has a much larger surface area. It receives the same pressure that was generated at the input piston.
The Incompressible Fluid
A fluid, typically oil, fills the chamber between the two pistons. Its job is to transmit the pressure from the input piston to the output piston without being compressed itself.
Putting It All Together: The Math of Force Multiplication
The relationship between the two sides of the press is direct and predictable.
The Input Side
When you apply an input force (F1) to the small piston with its area (A1), you create pressure (P) in the fluid.
The formula is: P = F1 / A1
The Output Side
This pressure (P) is transmitted throughout the fluid and pushes up on the large piston, which has a much larger area (A2). This generates the massive output force (F2).
The formula is: F2 = P * A2
The Multiplication Effect
Since the pressure (P) is the same on both sides, we can link the two equations. If we substitute the first equation into the second, we get:
F2 = (F1 / A1) * A2
This is most often written as: F2 = F1 * (A2 / A1)
This simple equation reveals everything. The output force is the input force, multiplied by the ratio of the areas of the two pistons. If the output piston's area is 100 times larger than the input piston's area, the output force will be 100 times greater than the force you applied.
Understanding the Trade-offs: There Is No Free Lunch
Hydraulic systems seem almost magical, but they operate under the laws of physics, specifically the conservation of energy. Force is multiplied, but it comes at a cost.
The Distance Trade-off
Work is defined as Force multiplied by Distance (Work = Force x Distance). To conserve energy, the work done on the input side must equal the work produced on the output side.
Because the output force is much larger, the distance it moves must be proportionally smaller. To lift the large piston by just one inch, you may need to push the small piston down by 100 inches.
The Speed Limitation
This distance trade-off directly results in a speed limitation. Hydraulic presses are incredibly powerful, but they are not fast. The large distance the input piston must travel to achieve a small movement on the output side makes the process inherently slow.
System Inefficiencies
In a perfect world, the work input would exactly equal the work output. In reality, some energy is always lost due to friction between the pistons and their cylinders, as well as the internal friction (viscosity) of the fluid itself.
Making the Right Choice for Your Goal
Understanding this principle allows you to see how hydraulic systems are designed for specific tasks.
- If your primary focus is maximum force multiplication: The design must maximize the ratio between the output piston's area and the input piston's area.
- If your primary focus is balancing force and speed: You must accept that an increase in operational speed (a greater output distance per pump) will always require a decrease in force multiplication.
By understanding how a constant pressure is leveraged across different areas, you can grasp the fundamental power of all hydraulic machinery.
Summary Table:
| Component | Role in Force Multiplication |
|---|---|
| Input Piston (Small) | Applies initial force to create high pressure in the fluid. |
| Hydraulic Fluid | Transmits pressure equally throughout the system (Pascal's Law). |
| Output Piston (Large) | Converts fluid pressure into a massively multiplied output force. |
| Area Ratio (A2/A1) | The multiplier factor; a larger ratio creates a greater output force. |
Need reliable, high-force equipment for your laboratory processes?
KINTEK specializes in lab equipment and consumables, serving laboratory needs with precision and durability. Our expertise ensures you get the right hydraulic or press equipment for your specific application, from material testing to sample preparation.
Let us help you achieve superior results with the right tools. Contact our experts today to discuss your requirements and discover how KINTEK can enhance your lab's capabilities.
